Graphics Dev Journal 1

A Journey Through Space Transformations

NOTE: THIS POST CONTAINS MATH ERRORS (12/14/2020)

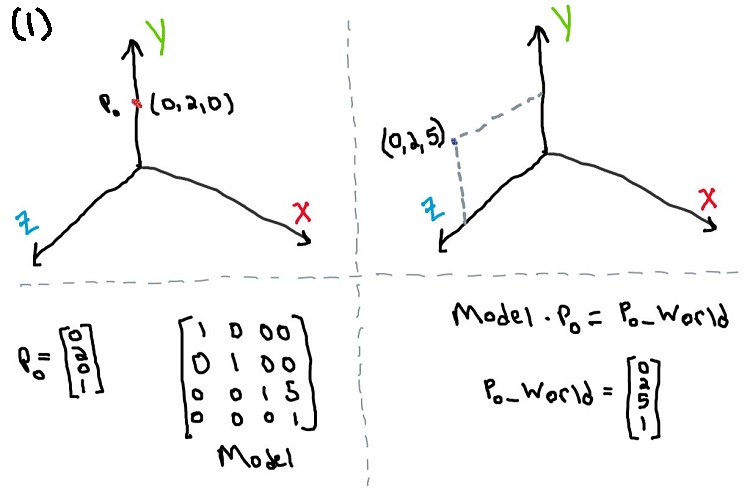
Say the point p0 is in object space and its coordinates are {0, 2, 0, 1} so just a point on the Y axis.

p0 is placed in world space by a model transformation shown in Figure 1, that is, no rotation, just translated along Z axis by 5 units.

The camera is sitting at the origin of world space but “looking” down the -Z axis, so the camera’s location in world space is c0 = {0, 0, 0, 1} and its coordinate system can be represented as shown in Figure 2, and then combining its location and coordinate system into view matrix also shown in Figure 2

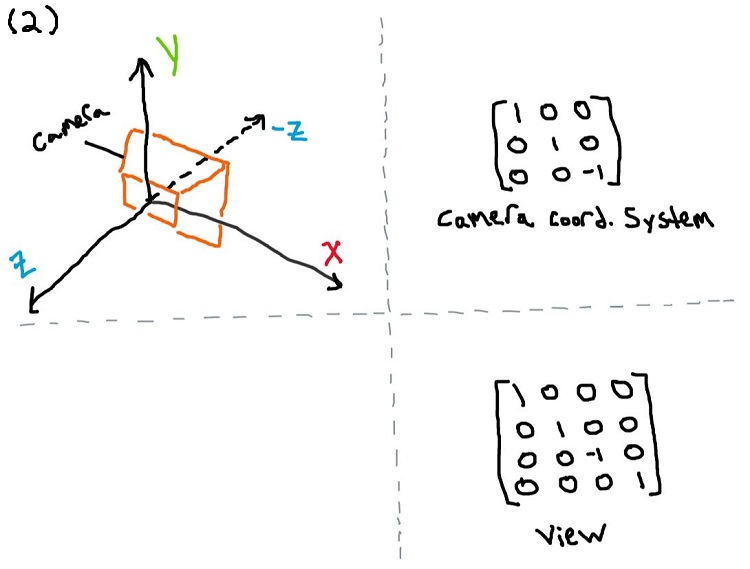
Note:

This is not a very sophisticated camera placement. It could be placed in the world and made to look at some point using a lookAt transformation. But to simply show the steps, I chose an easy camera location and chose a point I knew would be within view of the camera

To place p0_world (that is p0 transformed by model), into view space, it looks like the following. Note the sign change on the Z component after transforming from p0_world to p0_view.

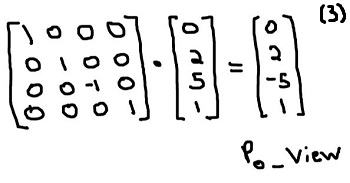
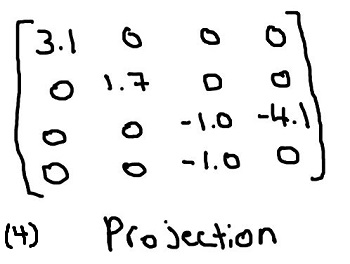
The next step is to put p0_view into projection space and to do that requires a projection matrix. Information about how projection matrices (in this case a perspective projection) are constructed can be found at reference 4. The required parameters are field of view (fov), near plane (zNear), and far plane (zFar), as well as the viewing screen’s width and height (more specifically aspect ratio). The projection matrix I came up with has the following parameters

• fov = 60 degrees

• aspect = 16:9

• zNear = 2

• zFar = 100

Which produces the resulting matrix shown in Figure 4

• Notes

  • Values have been rounded down to one significant figure
  • I have been laying out matrices in row major order

Transforming to projection space, or homogeneous clip space 1 is then accomplished by multiplying p0_view with the projection matrix

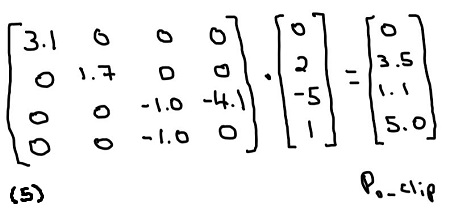
In the next step, divide the elements of p0_clip by its 4th element to transform into normalized device space 1. This produces p0_nds = {0.0, 0.7, 0.2, 1.0}

Finally convert to rasterization or view port space, using the calculations shown in Figure 6

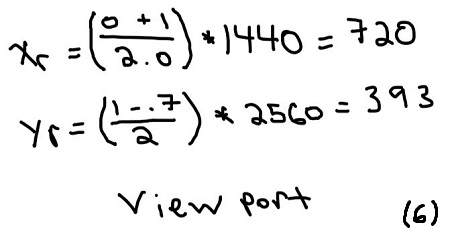
Looking at the result in Figure 6, it makes sense that the X coordinate is 720, because essentially the camera is sitting at {0, 0, 0} in world space, which transforms to the center of the view port i.e. {720, 1280}. Since p0_world had 0 displacement along the X, that should correspond to a value of 720 once projected onto the screen. Yay for 720!

The result is a 3D point that has been projection onto whatever screen you are viewing it from, in my case it was a phone screen.

Now the challenge is to to then take the point on the screen (or any point…at this point) and go back to 3D to see if it produces the original p0.

However, during the transformation to normalized device space, every element was divided by the w value of the vector (4th element). Then in the transformation to view port, the Z value was dropped because obviously there is no Z coordinate otherwise what the heck has all this been about.

So going back from 2D to 3D there is no unique solution. A more interesting exercise would be to ray cast from the 2D point caculated here, and to perform intersection/hit testing along this ray. Reference 1 goes over this, and perhaps another journey through transformations is in order.

• Notes

  • Vectors and points are represented by the notation {nx, ny, nz, w} where direction has w = 0 and point has w = 1, or {nx, ny, nz}

  • Starting from world space {0, 0, 0}, with camera at the origin, and some 3D point

References

[1] Mouse Picking with Ray Casting

[2] Computing 2D Coordinates of a 3D Point

[3] Convert world to screen coordinates

[4] Perspective Projection

Thanks for reading, feel free to send concerns and criticisms to me on Twitter